PRUEBAS ESTADÍSTICAS PARAMÉTRICAS

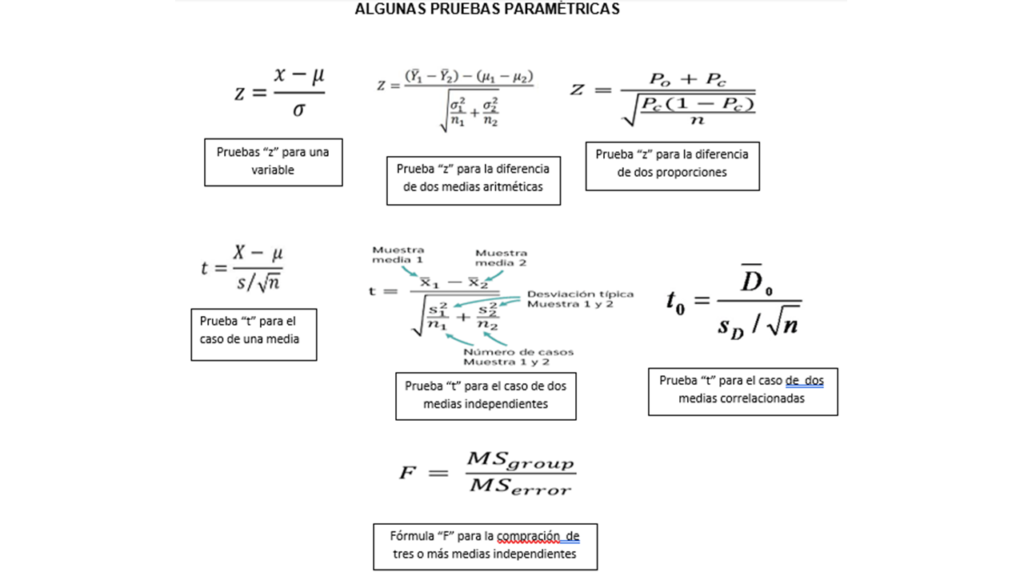
Para efectos de este artículo se definirá una distribución de probabilidad como un modelo matemático que describe las probabilidades asociadas con los posibles valores que se pueden obtener al medir una variable aleatoria; en otras palabras, cuál es la probabilidad de que ocurran estos valores.

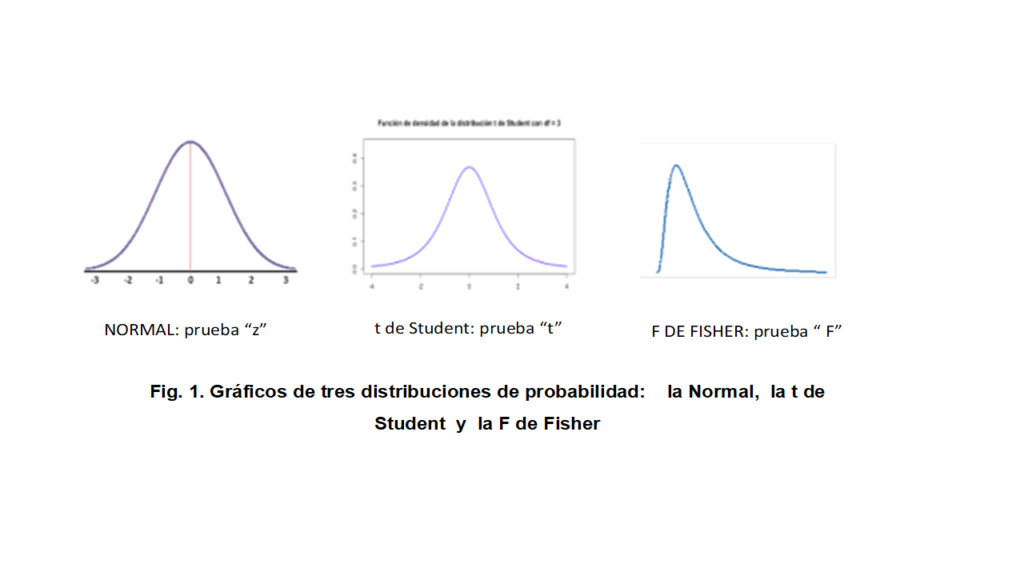
En la Figura 1 se observan las imágenes de tres distribuciones de probabilidad paramétricas, posiblemente las más utilizadas en investigación psicológica: la Normal, la F de Fisher y la t de Student. Cada una de ellas está asociada con uno o más tipos de pruebas estadísticas que permiten analizar los resultados de las investigaciones atendiendo a las características de las variables involucradas al momento de diseñar un estudio. Los investigadores debemos analizar las características estadísticas de las variables involucradas, para comprender e interpretar el posible comportamiento de los datos observados en el estudio. Una de las consecuencias de este análisis, es la aproximación de los datos a una de las distribuciones de probabilidad anteriormente señaladas. Al lograr esta aproximación, se está favoreciendo la identificación de la(s) prueba(s) estadística(s) correcta(s), además de la identificación de la distribución de probabilidad que permitirá una toma de decisión válida y confiable. La aproximación no es un aspecto que discutiremos en este artículo, pero se puede señalar que hay varios métodos para alcanzar el mismo, entre los cuales, uno de los más populares y sencillos, es a través de gráficas tales como los histogramas o los polígonos de frecuencia.

Volviendo al tema central del artículo, las pruebas estadísticas paramétricas, las mismas pueden ser definidas como aquellos procedimientos utilizados para la verificación de hipótesis sobre el comportamiento de las variables involucradas, atendiendo a ciertos supuestos relacionados con las poblaciones de las que provienen. Conversemos sobre estos supuestos.

Las variables de interés (las que se miden) deben ser continuas y estar medidas en una escala por lo menos de intervalos; o sea, debe ser capaz de asumir valores fraccionales y no solamente enteros dentro de un intervalo. Esto significa que los instrumentos de medición deben ser lo suficientemente precisos para medir la naturaleza propia de la variable. La escala de medición debe ser sensible a evaluar esta condición natural, lo cual facilitará le elección de la(s) prueba(s) estadística(s) paramétrica correspondiente(s).

En psicología se presenta frecuentemente la situación de que muchas “pruebas” arrojan puntuaciones enteras y no fraccionales. Sin embargo, si la variable está teóricamente definida como un constructo latente y si la misma presenta un número elevado de reactivos validados psicométricamente, la variable funciona como continua y se pueden aplicar pruebas paramétricas a sus resultados.

Los datos deben proceder de una población con distribución normal, o sea, que al graficarse los mismos, se observa que se aproximan a una forma de campana propio de la distribución normal de probabilidades. Sin embargo, esta propiedad se puede verificar a través de procedimientos de cálculos estadísticos.

 Otra condición que requieren las pruebas paramétricas es la homocedasticidad, que significa, que las varianzas entre varios grupos no son estadísticamente diferentes. Esta condición es básica al momento de comparar las medias aritméticas de dos o más grupos.

Las pruebas paramétricas están dirigidas a verificar hipótesis sobre datos poblacionales específicos llamados parámetros, aunque los mismos se analizan a través de los correspondientes datos obtenidos en las muestras llamados estadísticos; a cada parámetro poblacional, debe corresponder un estadístico muestral.  Las pruebas paramétricas evalúan el comportamiento de los parámetros poblacionales de manera indirecta, a través de sus correspondientes valores muestrales. Por ejemplo: la media poblacional (μ) se estima con la media muestral la desviación estándar poblacional (σ) se estima con la desviación estándar de la muestra (s), y así se procede con los otros parámetros considerados en el estudio.

Aunque los objetivos de este artículo no alcanzan los niveles estadísticos operativos, nos vamos a referir, de manera general, a algunas de las principales pruebas paramétricas y sus principales propiedades.

En primer lugar, nos referiremos a la prueba “z”, la cual está asociada con la distribución normal. Esta prueba estadística se utiliza preferiblemente con muestras con n> de 30 sujetos seleccionados aleatoriamente y se conoce el valor de la desviación estándar poblacional (σ). Si no se conoce la desviación poblacional puede utilizar la “s” de la muestra como aproximación; el Teorema Central del Límite favorece esta decisión. La prueba “z” se utiliza principalmente para pruebas de hipótesis en las cuales se intenta comparar la media de una muestra con una media poblacional, para comparar dos medias con el requisito de que se conozcan las desviaciones estándar de las poblaciones. La prueba “z” también se aplica para comparar las medias de dos muestras con n>30 y desviaciones estándar poblacionales conocidas. Además, se utiliza para comparar dos proporciones provenientes de muestras grandes. Es importante señalar que la utilización de esta prueba estadística paramétrica exige el cumplimiento de las propiedades de normalidad, homocedasticidad, aleatoriedad, continuidad de la variable y medición por lo menos en una escala de intervalos.

La prueba paramétrica t de Student está asociada con la distribución de probabilidades “t” de Student, y se utiliza para la comparación de medias aritméticas obtenidas en muestras pequeñas (n < ó = a 30) y con desviaciones estándar poblacionales desconocidas. Esta prueba utiliza la desviación estándar muestral como una estimadora de la desviación estándar poblaciónal. La distribución “t” es muy parecida a la normal en su forma de campana, también es simétrica, pero por estar asociada con muestras pequeñas, tiene propiedades particulares que la diferencian de la normal entre las cuáles se puede señalar que está definida por grados de libertad.  Una propiedad de la “t” es que a medida que “n” aumenta, sus características probabilísticas se aproximan a la norma estándar como consecuencia del Teorema Central del Límite, hasta llegar un momento en que los valores “t” son iguales a “z”.

La prueba F de Fisher se utiliza principalmente para la comparación de tres o más medias aritméticas, comparación de varianzas y la evaluación de modelos de regresión estadística.  Está asociada con la distribución de probabilidades “F”, que se define a través de grados de libertad para el numerador y para el denominador. Al igual que la Normal y la T, requiere que la(s) variable(s) sea continua(s), medida en una escala por lo menos de intervalos y que los sujetos sean seleccionados de manera aleatoria. La distribución es asimétrica positiva y los valores del estadístico F serán siempre positivos. Al igual que “t”, a medida que los grados de libertad aumentan, sus resultados se aproximan a la distribución normal.

No tenemos como objetivos de este artículo, el análisis detallado de las distribuciones de probabilidad paramétricas más importantes, ni los métodos de aplicación de las pruebas paramétricas más utilizadas. Nuestro interés es despertar la curiosidad en algunos estudiosos de la investigación del comportamiento con relación a las pruebas paramétricas y promover la investigación y profundización del conocimiento de estas importantes herramientas estadísticas al servicio de la investigación científica. En artículos posteriores nos referiremos a los mismos con un poco de más detalles.